Gradyan

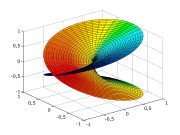
Bu şekiller açıktan koyuya doğru artan skaler alanları ve artışa doğru yönelmiş yöntürevi vektörünü göstermektedir.
Kalkülüs
Kalkülüs
Temel
Türev
İntegral

İntegral Alma Yöntemleri:
Çok değişkenli
Vektör hesabı

Bir skaler alanın yön türevi (gradyan) artımın en çok olduğu yere doğru yönelmiş bir vektör alanını verir ve büyüklüğü değişimin en büyük değerine eşittir.

Örneklemek gerekirse bir odadaki zamandan bağımsız sıcaklık dağılımı düşünülebilir. Sıcaklık dağılımı skaler bir alandır ve kartezyen koordinatlarda ϕ = ϕ ( x , y , z ) {\displaystyle \phi =\phi (x,y,z)\,} olarak gösterilebilir. Bu dağılımın yöntürevi en çok ısınan yeri işaret edecektir ve yöntürevi büyüklüğü de o yöndeki ısınmanın miktarını verecektir. Başka bir örnek olarak bir yokuş ele alınabilir. Yokuşa onu üstten kesen bir düzlemden bakılırsa ortaya çıkan fonksiyon yokuşun eğim profili H = H ( x , y ) {\displaystyle H=H(x,y)\,} 'i verir (basitlik için yokuşu iki boyutta düşünmek faydalı olacaktır). Bu fonksiyonun yöntürevi yokuşun en dik yerini, yöntürevinin büyüklüğü de bu yerin dikliğini verir.

Tanım

x genelleştirilmiş koordinatların kapalı gösterimi olmak üzere x = ( x 1 , … , x n ) {\displaystyle x=(x_{1},\dots ,x_{n})} bir f(x) fonksiyonunun yöntürevi

∇ f = ( ∂ f ∂ x 1 , … , ∂ f ∂ x n ) {\displaystyle \nabla f=\left({\frac {\partial f}{\partial x_{1}}},\dots ,{\frac {\partial f}{\partial x_{n}}}\right)}

şeklinde gösterilir. Burada ∇ {\displaystyle \nabla \,} , del işlemcisini temsil etmektedir. Başka bir gösterim ise grad' ftir.

Örnek

f ( x , y , z ) = x 3 + e 2 y − cos ⁡ ( w z ) {\displaystyle f(x,y,z)=x^{3}+e^{2y}-\cos(wz)\,} olmak üzere f fonksiyonunun gradyanı:

∇ f = ( ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z ) = ( 3 x 2 , 2 e 2 y , w sin ⁡ ( w z ) ) . {\displaystyle \nabla f={\begin{pmatrix}{\frac {\partial f}{\partial x}},{\frac {\partial f}{\partial y}},{\frac {\partial f}{\partial z}}\end{pmatrix}}={\begin{pmatrix}{3x^{2}},{2e^{2y}},{w\sin(wz)}\end{pmatrix}}.}

olarak elde edilir.

Bir göndermeyi doğrusallaştırma

Herhangi bir f(x) göndermeyi, bir x 0 {\displaystyle x_{0}} noktasında

g ( x ) = f ( x 0 ) + ( ∇ x f ( x 0 ) ) T ( x − x 0 ) {\displaystyle g(x)=f(x_{0})+(\nabla _{x}f(x_{0}))^{T}(x-x_{0})}

yaklaşımı yapılarak doğrusallaştırılabilir. g(x) doğrusu f(x) göndermesinin x 0 {\displaystyle x_{0}} noktasında doğrusallaştırılmış halidir.

Ayrıca bakınız

Kaynakça

  1. ^ Bachman, David (2007). Advanced Calculus Demystified. New York: McGraw-Hill. ISBN 978-0-07-148121-2. 

Dış bağlantılar